
Preview images of the first and second (if there is one) pages are shown.
#LATTICE MULTIPLICATION PDF#
Use the buttons below to print, open, or download the PDF version of the 4-Digit by 2-Digit Lattice Multiplication (A) math worksheet. Students can use math worksheets to master a math skill through practice, in a study group or for peer tutoring. Parents can work with their children to give them extra practice, to help them learn a new math skill or to keep their skills fresh over school breaks. Teachers can use math worksheets as tests, practice assignments or teaching tools (for example in group work, for scaffolding or in a learning center). It may be printed, downloaded or saved and used in your classroom, home school, or other educational environment to help someone learn math. This math worksheet was created on and has been viewed 26 times this week and 111 times this month. Try IE11 or Safari and declare the site as trusted in the Java setup.Welcome to The 4-Digit by 2-Digit Lattice Multiplication (A) Math Worksheet from the Long Multiplication Worksheets Page at. If you are reading this, your browser is not set to run Java applets. The length of the multiplicands is controlled by the Initial number of digits spin, but also may change as the number itself changes. , 0, or be made (the default) a part of the integer string so that, for example, if a digit changes from 9 to 0 its neighbor to the left accepts the carry of 1. The digits can change autonomously so that each will cycle through the values 1, 2, 3. There digits can be changed by dragging the cursor a little off center of each. The applet below offers an interactive version of the lattice multiplication. In the case of 124576×3857, the third intermediate sum 2 + 8 = 10 takes two digits leading to an additional carry of 1 which is added to the preceding sum 1 + 6 making it 1 + 6 + 1 = 8. So that the product can be read immediately: 4566×257 = 1173462. In a simpler case, of say, 4566×257, the lattice isĪnd adding the carry yields a one digit number in every cell: So that, for example, for the product 124576×3857, we'll have However, the 2-digit sums cause a complication which is resolved by carrying their first digit to the previous band and adding it to what remains there of the sum placed there previously.

Which tells us that the product 712×23 = 16376. If all the sums are single digit numbers, the product of the two multiplicands can be read right away by following the sums around the lattice counterclockwise: Naturally, it may happen that some of these sum are 2-digit numbers, as in the diagram. The sums are thought of as being ordered around the lattice, first from the top to the bottom and then left to right. The product 124576×3857 leads to the following diagram: The algorithm requires to compute the sums of all the digits in a band and place the result next to the lattice, to the left or below the bottom, as the case may be. Note that the diagonals split the lattice into (diagonal) bands:
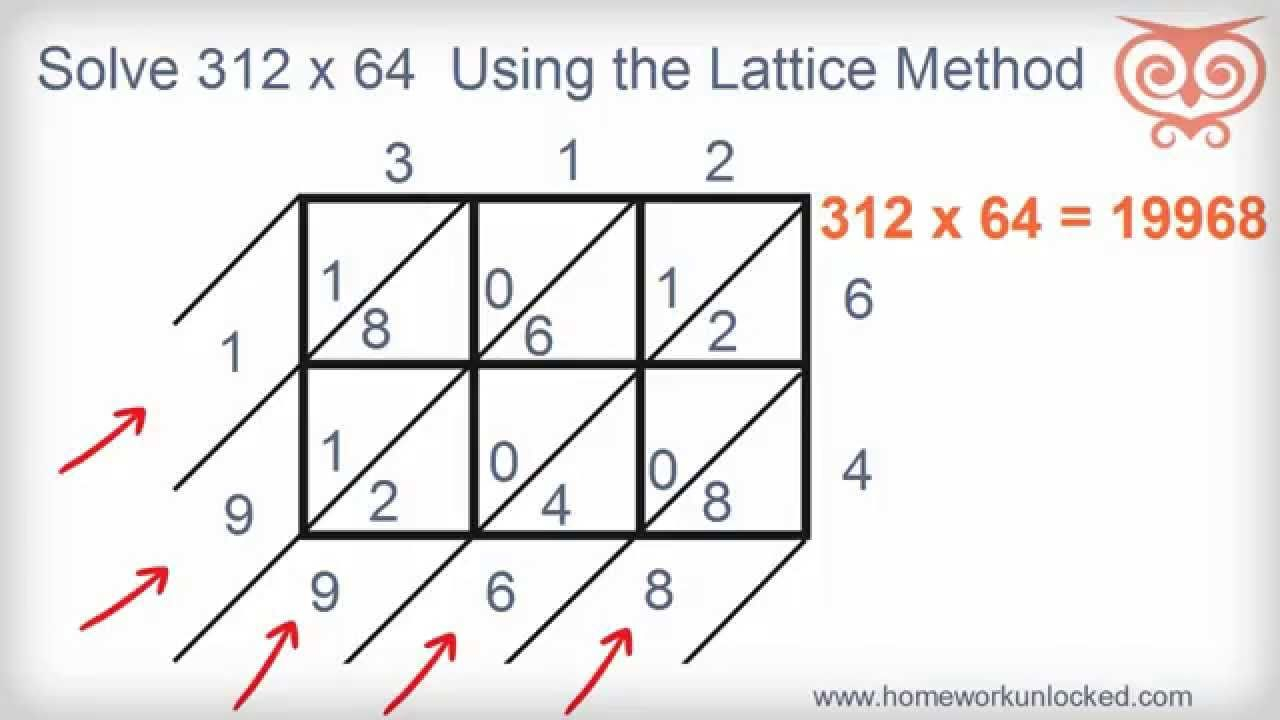
The 6 digits of 124576 are placed over six vertical columns, the 4 digits of 3857 generate four rows, and each cell holds the product of the corresponding digits of the two multiplicands. For example, the lattice below is made to help calculate 124576×3857: For example, this is a one cell lattice that shows the product 8×7:Ī bigger lattice may represent larger numbers. The number in the cell is the product of two digits, one placed above the cell, the other to its right. The method is so called because it requires a rectangular lattice with one of the diagonals drawn:Įach cell of the lattice is split by the diagonal into two parts used to house a 1- or 2-digit number.

It was introduced in Europe in 1202 by Leonardo Fibonacci in his Liber Abaci. Lattice multiplication is a predecessor of a more compact long multiplication scheme.


 0 kommentar(er)
0 kommentar(er)
